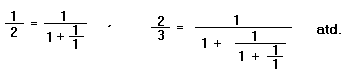Aritmetické hry
Výsledky
Úkoly:
- Na velkém jezeře jezdí bez přestávky dva vodní kluzáky.
Vypluly současně z protilehlých břehů: kluzák A od břehu B1
a luzák B od břehu B2.Poprvé se setkaly ve vzdálenosti
500 m od břehu B1, po druhé na zpáteční cestě ve vzdálenosti
300 m od břehu B2. Z těchto údajů určete délku jezera a poměr
rychlostí obou kluzáků. Důvtip vám pomůže vyřešit tuto ůlohu zpaměti, bez složitých výpočtů.
- Pět bojovníků z kmene Apačů v čele se slavným Vinnetouem zajalo 34 dobyvatelů - bělochů.
Do tábora je měli dopravit přes řeku v člunu, do kterého se věšlo 9 lidí.Náčelník Vinnetou
dal převést zajatce tak, aby jedn bojovník neměl pod dozorem více zjatců než 10 a aby je
převezli napětkrát.Víte, jak too učinil?
- Schůze začala mezi 6. a 7. hodinou večer a skončila mezi 9. a 10. hodinou.
Určete, v kterou hodinu schůze začala a v kterou skončila, víte-li ještě, že malá a velká si ručička si za tu dobu vyměnily místa.
- Bez dlouhého přemýšlení odpovězte na otázku: Kolik je půl druhé třetiny ze sta?
- Včely přeměňují nektar květůna med, přičemž z něho vylučují vodu. Nektar obsahuje přibližně 70% vody, získaný med je 17%. Kolik nejtaru musí včely nasbírat, aby získaly 1 kg medu?
-
Při hře vyzval Karel své dva přátele, Ondřeje a Toníka, aby si jeden vzal do ruky korunu a druhý padesátihaléř.
Potom řekl:
"Majiteli koruny dávám číslo 7 a majiteli padesátihaléře číslo 9. Ty, Ondřeji, násob své číslo dvěma a ty, Toníku, třemi. Sečtěte výsledky a řekněte mi součet nebo mi řekněte, zda je tento součet dělitelný třemi."
To stačilo Karlovi, aby určil, kdomá korunu a kdo padesátihaléř. Jak to uhádl?
-
Všechna čísla od 1 do 222 222 222 jsou napsaná jako posloupnost přirozených čísel. Kolikrát se vyskytne v zápisu těchto čísel nula?
-
Kalif z Bagdádu dovolil jednomu matematikovi, aby si přál co chce. Matematikse zatvářil nevině a řekl:
" Velký kalife, mám skromné přání. Odměň mě pšeničnými zrny, a to takto: Dej mi tolik pšeničných zrn, kolik jich bude muset být na posledním poli šachovnice, jestliže na první položíme jedno zrno a na každé následující dvojnásobek tohoto množství,
které bude na předcházejícím poli."
Kalif se zasmál a ochotně souhlasil. Domníval se, že matematik nedostane ani tlik zrní, aby si mohl upéci chleba. Velmi se však podivil, když matematik vypočítal, že jeho přání se nedá split.
Je to možné?
-
Jak dostaneme 100?
Máte použít číslic 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - každou jen jednou k sestavení dvou smíšených čísel (celé číslo se zlomkem) tak, aby jejich součet byl 100.
Úloha má několi řešení.
-
Leonardo Fibonacci z Pisy zkomal posloupnost čísel, ve které na prvním a druhém místě jsou jedničky a potom každé následující číslo se rovná součtu dvou předcházejících:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... .
Z těchto čísel utvořil zlomky tak, že dělil předcházející číslo následujícím:
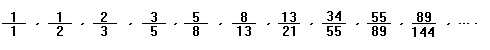
Tyto zlomky mají zajímavou vlastnost, a to takovou, že se dají vyjádřit pomocí samých jedniček, např.
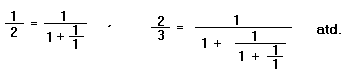
Pokuste se samy vyjádřit takto další zlomky.
-
Ve vlaku z Nitry do Bratislavy cestovalo v jednom oddělení šest cestujících. Jeden z nich bydlí v Nitře, jeden v Bratislavě, jeden v Komárně, jeden v levicích, jeden v Hlohovci a jeden v Trenčíně. Jejich jména začínají písmeny A, K, R, O, P a F. Nevíme však komu
které patří. Víme, že A a Nitřan jsou lékaři, P a Bratislavan jsou učitelé, Komárňan a R jsou inženýři, K a F náruživí sportovci, zatímco Komárňan nemá o sprtu ani poňetí. Hlohovčan je starší než A a Trenčíňan je starší než R. K a Nitřan vystoupili v Loepoldově,
R a Hlohovčan v Trnavě.
Určete povolání každého z těchto šesti cestujících a zároveň jejich bydliště.
-
Do hodinářské opravny přinesl zákazník čtvery hodiny: nástěnné, stolní, náramkové a budíka. Oznámil, ýe hodiny mají tyto závady: nástěnné hodiny se za 1 hodinu zpožďují o 2 minuty. Stolní hodiny předbíhají nástěnné za 1 hodinu o 2 minuty, budík se oproti stolním hodinám
opožduje za 1 hodinu o 2 minuty a náramkové hodinky předbíhají budík o 2 minuty za hodinu. O 12. hodině nastavili všechny hodiny na správný čas (podle časového signálu).
Kolik hodin bude na náramkových hodinkách v okamžiku časového signálu o 19. hodině?
-
Předtavte si, že píšete čísla od 1 za sebou tak, jak následují:
Která číslice stojí na tisícím místě? Jak to zjistíte?
-
Dvě přítelkyně se dohadovaly, kolik je které let. Jedna povídá: "Mně je právě dvakrát tolik let, kolik bylo tobě, když mně bylo tolik let, kolik je tobě nyní. Jakmile ti bude tolik le, koli je nyní mně, bude nám dohromady 63 let."
Kolik let bylo každé z nich?
-
Několik mužů, žen a dětí utratilo dohromady 20 mincí se stejnou hodnotou. kolik bylo mužů, žen a dětí, jestliže muž utratil 5 mincí, každá žena 3 mince a každé dítě půl mince?
-
Je možné za 5 sekund vynásobit číslo
a) 105 263 157 894 736 842 dvěma;
b) 1 034 482 758 620 689 655 172 413 793 třemi ?
Jak to dokážete?
-
Jestliže přečteme určité číslo zprava doleva, bude nové číslo čtyčiapůlkrát větší než dané číslo. Které číslo to je? Vyřešte tuto úlohu úsudkem, nikoli rovnicí.
-
Součin čtyř za sebou jdoucích přirozených čísel je 3024. Najděte tato čísla.
-
Tři přátelé se chystají na lyžařský zájezd. Zjistili, že jim ještě nějaké věci chybějí. Protože již měli málo času, poprosili sousedova chlapce. aby jim zaběhl do obchodu zakoupit chybějící potřeby, pro všechny tytéž. Každý mu dal 10 Kč.
Chlapec nakoupil, zaplatil 25 Kč a vrátil se zpět. Odevzdal nakoupené věci a chtěl vrátit i 5 Kč. Protože přinesl samé korunové mince, přátelé od něho vzali po koruně a 2 Kč mu nechali "od cesty". Při účtování však došlo k nedorozumění. Přátelé počítali: Chlapci jsme dali po 10 Kč; po 1 Kč nám však vrátil zpět.
Platili jsme tudíž 3*9 Kč = 27 Kč. dvě koruny dostal chlapec. Kde je další, třicátá koruna? Kde je chyba?
-
Ve starém Římě zemřel jeden muž a zanechal po sobě ženu, které se mělo narodit dítě. V závěti stanovil, že jestliže se narodí syn, má dostat 2/3 majetku a matka 1/3, jestliže se narodí dcera, má dostat 1/3 majetku a matka 2/3.
Vdově se narodila dvojčata, chlapec a děvče. Jak rozdělit majetek, aby to co nejvíce vyhovovalo podmínkám závěti?
-
Ze všech číslic od 1 do 9 (tudíž bez nuly) máme sestavit dvě čísla a jejich součin tak, aby se každá cifra použila jen jednou. Např.
28 * 157 = 4396.
Existují ještě další takové součiny? Pokuste se je vyhladat.
-
Na výletě vymýšleli studenti různé hry a zábavy. Ondřej-matematik dal spolužákům tuto hádanku: "Myslete si nějaké čtyřciferné číslo. Nyní přemístěte první číslici zleva na konec čísla. Dostanete další čtyřciferné číslo. První číslo sečtěte s tímto nově utvořeným číslem a řekněte mi výsledek."
karel hlásil 8612, Gustav 4322, Toník 9867 a Olga 13859.
"Dobře počítal jen Toník, všichni ostatní počítali špatně", prohlásil Ondřej.
Přeskoušeli výsledek a skutečně. Odřej měl pravdu. Jak na to přišel?
Výsledky